FIGURAS PLANAS

En las figuras planas se puede calcular el perímetro que es la medida del contorno de una figura y el área que es la medida de la superficie que esta figura ocupa.

Llamaremos al perímetro de la siguiente forma: $2p$
Y al área: $A$
Podemos dividir a las principales figuras planas según el número de lados, de esa forma tenemos:

Cuadriláteros

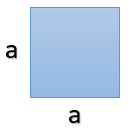
Rectángulo Donde: "a": es la medida de la altura "b": es la medida de la base Podemos decir: $$2p=2a+2b$$ $$A=a \cdot  b$$	Cuadrado Donde: "a": es la medida de uno de los lados Podemos decir: $$2p=4a$$ $$A=a^{2}$$
Paralelogramo Donde: "d": es la medida de la diagonal menor "D": es la medida de la diagonal mayor Podemos decir:$$A=\frac{d\cdot D}{2}$$	Rombo Donde: "a": es la medida de la altura "b": es la medida de la base Podemos decir: $$A=ab$$
Trapecio Donde: "a": es la medida de la altura "M": es la medida de la base mayor "m": es la medida de la base menor Podemos decir: $$A=a \cdot \left ( \frac{M+m}{2} \right )$$

Triángulos

Tenemos tres tipos de triángulos según la medida de los ángulos internos:

• El acutángulo donde todas las medidas de sus ángulos son menores a 90°
• El rectángulo donde la medida de uno de sus lados es 90°
• El obtusángulo donde la medida de uno de sus lados supera los 90°

Donde:

• "a": es la medida de la altura
• "b": es la medida de la base

Podemos decir:
$$A=\frac{a \cdot  b}{2}$$

Figuras regulares de más de 4 lados

Para calcular su perímetro simplemente se multiplica la medida de su lado por la cantidad de lados, pero para el cálculo de su área se necesita conocer la medida de su apotema que es una altura trazada desde el centro de la figura hacia alguno de sus lados.

Donde:

• "a": es la medida de uno de sus lados
• "ap": es la medida de la apotema
• "n": es el número de lados de la figura

Podemos decir:
$$2p=n \cdot a$$

$$A=\frac{2p \cdot  ap}{2}$$

Circunferencia y círculo

Donde:

• "R": es la medida del radio

Podemos decir:
$$2p=2\pi \cdot R$$

$$A=\pi \cdot  R^{2}$$

TABLA DE DERIVADAS

Derivadas directas

---

Función	Derivada	Ejemplo
$$y=k$$	$$y'=0$$	$$y=5$$ $$y'=0$$
$$y=kx$$	$$y'=k$$	$$y=-10x$$ $$y'=-10$$
$$y=x^{k}$$	$$y'=kx^{k-1}$$	$$y=x^{5}$$ $$y'=5x^{4}$$
$$y=ax^{k}$$	$$y'=(a\cdot k)x^{k-1}$$	$$y=-2x^{3}$$ $$y'=-6x^{2}$$
$$y=ln(U(x))$$	$$y'=\frac{U'(x)}{U(x)}$$	$$y=ln(4x^{2})$$ $$y'=\frac{8x}{4x^{2}}=\frac{2}{x}$$
$$y=log_{a}U(x)$$	$$y'=\frac{U'(x)}{U(x)} \cdot log_{a}e$$	$$y=log_{5}3x^{3}$$ $$y'=\frac{9x^{2}}{3x^{3}} \cdot log_{5}e=\frac{3 \cdot log_{5}e}{x}$$
$$y=e^{U(x)}$$	$$y'=e^{U(x)} \cdot U'(x)$$	$$y=e^{(4x^{5})}$$ $$y'=e^{(4x^{5})} \cdot (20x^{4})$$
$$y=a^{U(x)}$$	$$y'=a^{U(x)} \cdot U'(x) \cdot Ln(a)$$	$$y=7^{(4x^{5})}$$ $$y'=7^{(4x^{5})} \cdot (20x^{4})\cdot Ln(7)$$

Derivadas de funciones compuestas

---

Suma y resta de funciones

En este caso cada termino de la funcion compuesta se deriva por separado aplicando las derivadas directas

Ejemplo: $$y=2x^{34}-\sqrt[3]{2x^2}+e^{2x}$$ La derivada de esta función se puede calcular hallando la derivada de cada uno de sus términos por separado: $$\frac{dy}{dx}=\frac{d(2x^{34})}{dx}-\frac{d((2x^2)^{\frac{1}{3}})}{dx}+\frac{d(e^{2x})}{dx}$$ $$y'= 68x^{33}-(2x^2)^{\frac{-2}{3}} \cdot 4x + e^{2x} \cdot 2 $$ $$y'=68x^{33}- \frac{4x}{\sqrt[3]{4x^4}}+ 2 \cdot e^{2x}$$

Producto de funciones

Función	Derivada
$$f(x) = U(x) \cdot V(x)$$	$$\frac{d(f(x))}{dx} = U'(x) \cdot V(x) + U(x) \cdot V'(x)$$

Ejemplo:
$$y=(2x+11)(e^{3x})$$ Su derivada: $$y'=\frac{d(2x+11)}{dx} \cdot (e^{3x})+\frac{d(e^{3x})}{dx} \cdot (2x+11)$$ $$y'=2 \cdot e^{3x}+ 3e^{3x} \cdot (2x+11)$$

Cociente de funciones

Función	Derivada
$$f(x) = \frac{U(x)}{V(x)}$$	$$\frac{d(f(x))}{dx} = \frac{U'(x) \cdot V(x) - U(x) \cdot V'(x)}{(V(x))^{2}}$$

Ejemplo:
$$y=\frac{2x+11}{e^{3x}}$$ Su derivada: $$y'=\frac{\frac{d(2x+11)}{dx} \cdot (e^{3x})-\frac{d(e^{3x})}{dx} \cdot (2x+11)}{(e^{3x})^2}$$ $$y'=\frac{2 \cdot e^{3x}- 3e^{3x} \cdot (2x+11)}{e^{6x}}$$