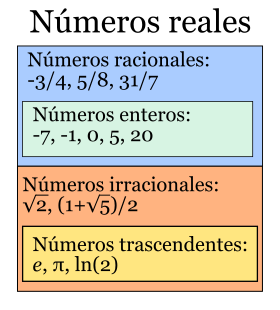
¿QUÉ ES UN NÚMERO?
Un número, en ciencia, es una abstracción que representa una cantidad o una magnitud. En matemáticas un número puede representar una cantidad métrica o con mayor frecuencia un elemento de un sistema numérico o un número ordinal que representará una posición dentro de un orden de una serie determinada. Este tiene un grafo, nosotros adoptamos los números arábigos, pero existen otras como los números Romanos, o de idiomas asiáticos.
¿CÓMO SE ORGANIZAN LOS CONJUNTOS NUMÉRICOS?
De manera general podemos organizarlos de la siguiente manera:
Números naturales:
Son aquellos números enteros y positivos, aún hay cierta discrepancia entre incluir dentro de los mismos al número cero. Por ahora nosotros no vamos a incluirlo.
Por lo tanto estos números serían: $$ 1, 2, 3, 4, 5, 6, ... $$
Se les representa por la letra ℕ
Podemos definir la adición de naturales, puesto que la suma de dos naturales, nos dará otro natural.
2 + 5 = 7
La sustracción puede ser definida pero teniendo en cuenta que el Minuendo debe ser mayor que el sustraendo, caso contrario el resultado sería negativo y los números negativos no están considerados en los naturales.
5 - 2 = 3
2 - 5 = - 3 (Pero el " -3 " no está definido en los naturales)
También podemos definir la multiplicación, puesto que multiplicar dos naturales nos da otro natural, eso nos da paso a definir la potenciación, pero con exponente natural o cero.
En el caso de la división, se puede definir pero solo cuando el cociente resulte entero:
15 : 3 = 5
3 : 15 = 0,2 (Pero el "0,2" no esta definido en los naturales)
Números enteros:
Están compuestos por los números naturales, además de incluir al cero y los números negativos.
Por lo tanto estos números serían: $$ ..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, ... $$
Se les representa por la letra ℤ
Podemos definir la adición, sustracción y multiplicación. Ambos cumplen la propiedad de Clausura.
También podemos definir la multiplicación, puesto que multiplicar dos naturales nos da otro natural, eso nos da paso a definir la potenciación, pero con exponente natural o cero.
"Al igual que en los naturales, con la diferencia que la base si puede ser negativa"
En el caso de la división, se puede definir pero solo cuando el cociente resulte entero:
15 : ( - 3) = - 5
3 : 15 = 0,2 (Pero el "0,2" no esta definido en los enteros)
Números Racionales:
Están compuestos por los números naturales, además de incluir al cero y los números negativos y definen el concepto de fracción, de esta manera incluyen a los números decimales.
Por lo tanto estos números serían:
$$Q=\left\{ { \frac { p }{ q } }\quad|\quad{ p,q\quad \in \quad Z\quad \curlywedge \quad q\quad \neq \quad 0 } \right\} $$
Se les representa por la letra ℚ
Podemos definir la adición, sustracción, multiplicación y división. Ambos cumplen la propiedad de Clausura. Dentro de este grupo se definen los decimales exactos, periódicos puros y mixtos.
En el caso de la potenciación la base puede ser positiva y negativa, además el exponente puede ser entero positivo o negativo, para los exponentes fraccionarios, solo están definidos dentro de los racionales si el resultado no es irracional.
Números Irracionales:
un número irracional es un número que no puede ser expresado como una fracción m/n, donde m y n son enteros y n es diferente de cero. Es cualquier número real que no es racional. Un decimal infinito aperiódico, como:
$$\sqrt { 3 } =1,732050808...$$
No puede representar un número racional. A tales números se los nombra «números irracionales». Esta denominación significa la imposibilidad de representar dicho número como razón de dos números enteros.
Los números reales que no son racionales se llaman irracionales. Su conjunto se denota por 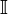 .
.
Se clasifican en dos tipos:
Número algebraico: Son la solución de alguna ecuación algebraica y se representan por un número finito de radicales libres o anidados en algunos casos.
Número trascendente: No pueden representarse mediante un número finito de raíces libres o anidadas; provienen de las llamadas funciones trascendentes: trigonométricas, logarítmicas, exponenciales, etc. También surgen al escribir números decimales no periódicos al azar o con un patrón que no lleva periodo definido, respectivamente.
Los llamados números trascendentes tienen especial relevancia ya que no pueden ser solución de ninguna ecuación algebraica. Los números pi y e son irracionales trascendentes, puesto que no pueden expresarse mediante radicales.
Números Reales:
En matemáticas,el conjunto de los números reales, denotado por ℝ, incluye tanto a los números racionales: positivos, negativos y el cero; como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales aperiódicas, tales como: √5, π, el número real log2, cuya trascendencia fue enunciada por Euler en el siglo XVIII.
Dicho en palabras más sencillas, los números reales son un conjunto dentro del cual se encuentras los números racionales e irracionales.
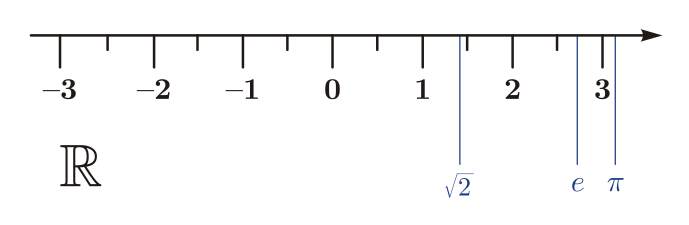
Podemos observar una recta real, en la cual se observan números naturales, enteros, racionales e irracionales:
En los números reales están definidas las operaciones como: la adición, sustracción, división, multiplicación, potenciación y la radicación.
Aunque estas dos ultimas tienen condiciones:
- Potenciación: No se encuentra definido el número 0 elevado a la potencia 0.
- Radicación: La raíz con indice par de un número negativo
Números Complejos:
Es una composición de un número imaginario "i" y un número real, de la siguiente forma:
$$ a+bi $$
Donde :
$$ i=\sqrt { -1 } $$
En este conjunto se define la raíz con indice par de un número negativo.
OPERACIONES BÁSICAS
ADICIÓN Y SUSTRACCIÓN EN ENTEROS
Si los números enteros tienen el mismo signo, se suman los valores absolutos y al resultado se le coloca el signo común.
3 + 5 = 8
−3 + −5 = − 8
Si números enteros son de distinto signo, se restan los valores absolutos -al mayor le restamos el menor- y al resultado se le coloca el signo del número de mayor valor absoluto.
− 3 + 5 = 2
3 + −5 = − 2
La diferencia de los números enteros se obtiene sumando al minuendo el opuesto del sustraendo.
7 − 5 = 2
7 − − 5 = 7 + 5 = 12
ADICIÓN Y SUSTRACCIÓN DE DECIMALES
Se debe alinear los números de acuerdo a la coma decimal, completando los espacios faltantes con ceros:
ADICIÓN Y SUSTRACCIÓN DE FRACCIONES
Partimos de la definición de fracciones homogéneas y heterogéneas, dependiendo del caso se seguira de diferentes maneras:
HOMOGÉNEAS:
$$ \frac { 5 }{ 2 } +\frac { 7 }{ 2 } =\frac { 5+7 }{ 2 } =\frac { 12 }{ 2 } =6 $$
Como observamos el denominador NO se suma, permanece igual, al final simplificamos si es posible
$$ \frac { 5 }{ 2 } -\frac { 7 }{ 2 } =\frac { 5-7 }{ 2 } =\frac { -2 }{ 2 } =-1 $$
HETEROGÉNEAS:
Hay tres formas de resolver, la primera es una multiplicación cruzada, se multiplican los denominadores y luego numerador con denominador de la otra fracción, es práctica cuando se tiene denominadores primos entre sí, y generalmente se usa cuando son solo dos fracciones las que se suman.
$$ \frac { 5 }{ 2 } -\frac { 7 }{ 3 } =\frac { 5\times 3-7\times 2 }{ 2\times 3 } =\frac { 15-14 }{ 6 } =\frac { 1 }{ 6 } $$
La segunda forma es la tradicional, sacando el MCM a los denominadores, luego ese resultado es el denominador de la fracción resultante, el cual divide cada denominador de las fracciones iniciales y multiplica a los numeradores de los mismo para obtener las numeradores parciales que serán operados según el caso. Es más utilizada con más de dos fracciones que se operan.
$$ \frac { 1 }{ 5 } +\frac { 5 }{ 8 } -\frac { 7 }{ 12 } $$
$$ \frac { 1 }{ 5 } +\frac { 5 }{ 8 } -\frac { 4 }{ 12 } =\frac { (120\div 5)\times 1+(120\div 8)\times 5-(120\div 12)\times 7 }{ 120 } $$
$$\frac { (24)\times 1+(15)\times 5-(10)\times 7 }{ 120 } =\frac { 24+75-70 }{ 120 } =\frac { 29 }{ 120 } $$
MULTIPLICACIÓN Y DIVISIÓN
Tengamos en cuenta que la multiplicación tiene como propósito simplificar sumas sucesivas, permitiéndonos realizar cálculos con mayor facilidad
REGLA DE SIGNOS
Es muy importante saber que el signo resultante al aplicar estas dos operaciones no es igual que cuando realizábamos una adición o sustracción, se cumple lo siguiente:
MULTIPLICACIÓN Y DIVISIÓN EN ENTEROS
La multiplicación de varios números enteros es otro número entero, que tiene como valor absoluto el producto de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos.
3 · 5 = 15
(−3) · (−5) = 15
3 · (−5) = − 15
(−3) · 5 = − 15
La división de dos números enteros no necesariamente será entero, y tiene como signo el que se obtiene de la aplicación de la regla de los signos.
30 : 5 = 6
(−30) : (−5) = 6
30 : (−5) = − 6
(−30) : 5 = − 6
Dividir dos número enteros, no nos da siempre como resultado otro entero, por ello definimos decimales y fracciones.
MULTIPLICACIÓN Y DIVISIÓN DE DECIMALES
Para multiplicar dos números decimales, realizamos la multiplicación como si no hubiera decimales. En el resultado, contamos la cantidad de decimales que poseen ambos factores y esa cantidad de decimales en total, es la cantidad de decimales que tendrá el producto.
Para el caso de la división, muchos eliminan las comas del divisor, pero en mi experiencia, el tener aún coma en el dividendo genera confusión en el desarrollo del ejercicio muchas veces, recomiendo eliminar todas las comas, multiplicando ambos , tanto dividendo como divisor por un múltiplo de 10, tal que se eliminen todos los decimales:

MULTIPLICACIÓN Y DIVISIÓN DE FRACCIONES
La multiplicación de fracciones, se realiza de manera directa: es decir, se multiplica numerador con numerador y denominador con denominador:
$$\frac { 3 }{ 4 } \times \frac { 6 }{ 5 } =\frac { 3\times 6 }{ 4\times 5 } =\frac { 18 }{ 20 } =\frac { 9 }{ 10 }$$
En el caso de la división, si invertimos la segunda fracción, podemos operar como si fuera una multiplicación, recordando que la multiplicación por el inverso multiplicativo de un número es una forma de expresar una división, siempre y cuando ese número sea diferente de cero.
$$\frac { 3 }{ 4 } \div \frac { 6 }{ 5 } =\frac { 3 }{ 4 } \times \frac { 5 }{ 6 } =\frac { 3\times 5 }{ 4\times 6 } =\frac { 15 }{ 24 } =\frac { 5 }{ 8 } $$
Otra forma es colocar una fracción sobre la otra, y aplicar un método llamado "extremos y medios", donde se multiplican los extremos y el resultado es el numerador, y luego los medios cuyo resultado es el denominador:
$$\frac { 3 }{ 4 } \div \frac { 6 }{ 5 } =\frac { \frac { 3 }{ 4 } }{ \frac { 6 }{ 5 } } =\frac { 3\times 5 }{ 4\times 6 } =\frac { 15 }{ 24 } =\frac { 5 }{ 8 } $$
PAUTAS PARA OPERACIONES COMBINADAS
¿Cómo resolver una operación combinada?
1º Efectuar las operaciones entre paréntesis, corchetes y llaves, de adentro hacia afuera.
2º Calcular las potencias y raíces, reconocer algunos teoremas para potencias y/o raíces sucesivas
3º Efectuar los productos y cocientes, recomiendo de izquierda a derecha, recordar que el divisor es el inverso multiplicativo de un número.
4º Realizar las sumas y restas, recomiendo de izquierda a derecha, caso contrario tener sumo cuidado en los signos
Enlaces a ejercicios:
Enteros
Decimales y fracciones




































 .
.