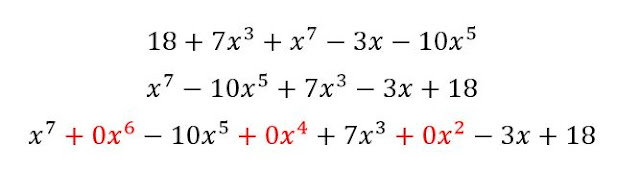INFOGRAFIAS SOBRE FUNCIONES

FUNCION LINEAL: (clic aquí)

FUNCION CUADRATICA: (clic aquí)

 

POTENCIACIÓN Y RADICACIÓN

Potenciación

La potenciación nos sirve para realizar multiplicaciones sucesivsa de un mismo número

$$ a^n $$
Donde
n: exponente
a: base

Radicación

La radicación para hallar la inversa de la potenciación

$$\sqrt[n]{a}$$
Donde
n: índice 
a: base

Ambas tienen sus propiedades, pero conociendo y aplicando las propiedades de la potenciación, podemos trabajar con las de la radicación sin complicarnos demasiado.

TEOREMAS

Considerando que: $a \in \mathbb{R}$

Exponente cero

$ a^{0}=1 $ Se cumple para: $a\neq 0$

Exponente unitario

$ a^{1}=a $

Exponente negativo

$ a^{-1}=\frac{1}{a} $ Se cumple para:  $a\neq 0$

Producto y cociente de bases iguales

$ a^{b}.a^{c}=a^{b+c}$

$ \frac{a^{b}}{a^{c}}=a^{b-c} $ Se cumple para: $a\neq 0$

Potencia de potencia con paréntesis

$ (a^{b})^{c}=a^{bc}$

Producto y cociente elevados a una potencia común

$ (a.b)^{c}=a^{b}.b^{c}$

$ (\frac{a}{b})^{c}=\frac{a^{c}}{b^{c}} $ Se cumple para: $b\neq 0$

Exponente fraccionario

$ a^{\frac{b}{c}}=\sqrt[c]{a^{b}} $

Producto y cociente con índice común

$ \sqrt[c]{a.b}=\sqrt[c]{a}.\sqrt[c]{b} $

$ \sqrt[c]{\frac{a}{b}}=\frac{\sqrt[c]{a}}{\sqrt[c]{b}} $ Se cumple para: $b\neq 0$

Raices sucesivas

 $ \sqrt[b]{\sqrt[c]{a}}=\sqrt[b.c]{a} $

MÉTODO DE RUFFINI

MÉTODO DE RUFFINI

El algoritmo de Ruffini es un método para la obtención del cociente y residuo de un polinomio entre otro de menor grado absoluto, para nuestro caso, vamos a observar de manera inicial polinomios con una sola variable, y además el polinomio divisor es de grado uno.

Aprenderemos los pasos a través del siguiente ejemplo:

Primero: El polinomio debe ser completo y ordenado de manera descendente, lo completamos añadiendo los términos que faltan con ceros.

Segundo: Nos valemos de un cuadro, puede ser este o cualquiera otro similar, cada maestro, libro, pagina web, etc. Utilizará uno diferente, yo empleo el utilizado para el "Método de Horner", para tener ambos relacionados.

Tercero: Colocamos los coeficientes del numerador en la parte intermedia superior del cuadro, el ultimo coeficiente se coloca en la ultima de todas, esa ultima linea nos sirve para diferenciar entre el cociente y el residuo; en la parte izquierda al medio se despeja la variable "x", el valor obtenido se coloca en esa parte.

Cuarto: Bajamos el primer coeficiente.

Quinto: Multiplicamos ese coeficiente por el coeficiente divisor despejado (en nuestro caso el 3) y lo colocamos debajo del siguiente término.

Sexto: Sumamos los dos coeficientes, y repetimos el proceso anterior.

Por ultimo repetimos el proceso hasta completar la tabla

Para obtener el cociente, se trabaja los coeficientes obtenidos en la parte intermedia, y el residuo es el número resultante en la parte final:

Valor Absoluto

¿Qué es el valor absoluto?

Plantearnos esta pregunta suele ser un poco tedioso, pero la verdad es que el valor absoluto de un número es simplemente el número sin su signo.

Por ejemplo: el valor absoluto de " -5 " es  " 5 " y si me preguntaran el valor absoluto de " +5 " es " 5 ", lo cual implica que sí, efectivamente el número se convierte en positivo de alguna manera.

OJO: se utiliza en la nomenclatura unas barras laterales, dentro de las cuales va el valor: $$ |  | $$ó en casos de programación una función: "$$abs( ) $$", el valor va dentro de los paréntesis, llaves o corchetes.
Ejemplos:
$$| - 10 | = 10$$
$$abs (-40) = 40$$

Pero que sucede cuando tenemos incógnitas afectadas por el valor absoluto, y más aún si tenemos toda una expresión afectada por el mismo, bien en ese caso, al ser una incógnita o una expresión, los resultados son infinitos, pero podemos hallar puntos críticos, para que me sirven estos, pues bien todos nos lo preguntamos alguna vez, estos nos ayudarán en la resolución de ecuaciones e inecuaciones con valor absoluto.

Definir un valor absoluto

Hay una forma de definir un valor absoluto, es teniendo un valor elevado al cuadrado, y luego este siendo operado por la raíz cuadrática:

$$\sqrt[2]{a^2}$$

A simple vista eliminaríamos la potencia y la raíz y nos quedaría el valor tal cual, pero les planteo estos casos:

$$\sqrt[2]{4^2} = \sqrt[2]{16} = 4$$
$$\sqrt[2]{(-4)^2} = \sqrt[2]{16} = 4$$

Como se observa, sea el número positivo o negativo, el valor final es 4, lo cual nos lleva a reflexionar sobre esta manera de definir un valor numérico.

Propiedades