ELIPSE

ECUACIÓN DE LA ELIPSE

Dependiendo de la orientación de la elipse tendremos dos formas de expresar su ecuación.

Si la elipse es horinzontal:

La ecuación será:

$$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$$


Los valores de $a$, $b$ y $c$ se hallan mediante un teoréma de pitágoras:

$$a^{2}=b^{2}+c^{2}$$

Nota:

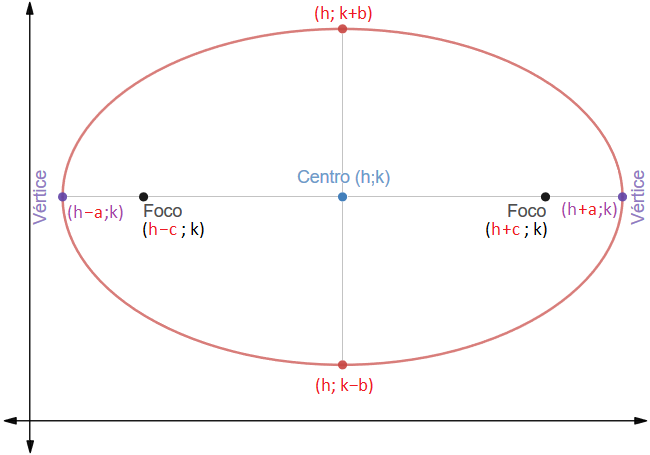
• Los vértices del eje mayor, los focos y el centro se encuentran alineados en el eje "x", es decir, el valor de $k$ no varía para ninguno.
• Los vértices del eje menor y el centro están alineados con el eje "y", por lo cual el valor de $h$ permanece constante en los tres.

Si la elipse fuera vertical

 

La ecuación será:

$$\frac{(y-k)^{2}}{a^{2}}+\frac{(x-h)^{2}}{b^{2}}=1$$

Los valores de $a$, $b$ y $c$ se hallan mediante un teoréma de pitágoras:

$$a^{2}=b^{2}+c^{2}$$

Nota:

• Los vértices del eje mayor, los focos y el centro se encuentran alineados en el eje "y", es decir, el valor de $h$ no varía para ninguno.
• Los vértices del eje menor y el centro están alineados con el eje "x", por lo cual el valor de $k$ permanece constante en los tres.